Muitos não sabem, mas a matemática está tendo uma grande contribuição no combate a pandemia covid-19. Por exemplo, sabe-se que 779 casos de covid-19 teriam sido exportados na China até 15 de fevereiro, e daí para cá o vírus se espalhou no Brasil.

A Modelagem Matemática é um método onde trazemos a matemática na teoria abstrata para a vida prática, ou seja, é este modelo matemático que está sendo utilizado no Coronavírus. Vamos entender as funções da modelagem matemática aplicada na escola, trazida para a vida prática:

Interação: é o reconhecimento se o problema escolhido pode se transformar em uma aprendizagem significativa com o mundo real.

Matematização: é o reconhecimento da situação problema, mostrando para o aluno que a modelagem na direção de um modelo.

Modelo matemático: é a Interpretação da solução, ou seja, com os dados propostos no problema deve-se haver uma interpretação e achar a solução concreta;

Situação: é a modelagem matemática abstrata e precisamos transformar em um modelos matemáticos válidos.

Formulação do problema: é criar hipóteses de que esta formulação seja capaz de modelar, obter uma resolução e validação.

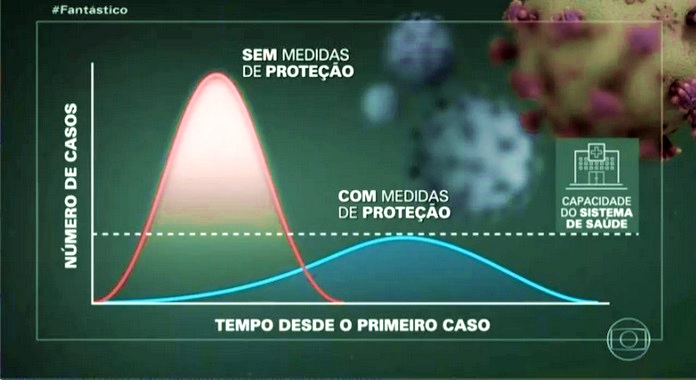
No combate o coronavírus é a modelagem matemática que faz projeções sobre a disseminação da doença, o número de infectados, a porcentagem de mortes e ainda simula as intervenções mais eficientes para proteger a população. Em vez de tratar pacientes e prescrever remédios, usam-se números e modelos estatísticos para entender como as doenças se espalham, e projetar quantos podem se contaminar em um determinado período.

Como funciona na prática?

Por meio de um gráfico exponencial, ou outro modelo de dados podemos simular o número de pessoas que vão se infectar em um determinado período, com base num modelo matemático obtermos informações importantes entre elas: o número da população de uma Cidade, ou Estado e quantos hospitais (leitos) existem? O número de infectado é X e o número de leitos é Y, e o número mortes é Z, mas quero projetar daqui para frente, para tomar as devidas providencias. Vamos pegar um exemplo do Estado de São Paulo, que é o epicentro da doença, com base no número de mortes e número de infectados e porcentagem de isolamento, dar para nos ter uma aproximação de como irá ficar a situação.

Um modelo que o Estado de São Paulo está usando é o modelo matemático por amostragem (estatístico), ou seja, estatisticamente falando se o número de isolamento desce, o número de infectados sobe. E se o número de infectado sobe, o número de mortes também sobe é o que está acontecendo.

Por exemplo, o estado de São Paulo registrou, no dia 23 de Abril o recorde no número de mortes causadas pela covid-19 em 24 horas, foram 211, um salto de 414% em relação aos 41 óbitos computados no dia anterior (22/04).

Ocupação de UTIs e leitos

Sabendo-se que tenho um determinado número de leitos, dar-se para calcular a porcentagem de ocupação, e se aumentar o número de infectados irá faltar leitos, na prática São Paulo já encara este problema. O governo de São Paulo, projeta que cerca de 1% da população, ou seja, cerca de 460 mil pessoas, será infectada. Já as internações devem variar entre 23 e 46 mil casos, que podem ser absorvidas, se chegarem gradativamente aos hospitais.

Os modelos matemáticos antecipa o potencial colapso, que é a Modelagem matemática que descreve um fenômeno matematicamente utilizando equações. A modelagem simula um certo processo ou objeto do mundo real para estabelecer prognósticos.

Como se calcula a taxa disseminação do vírus?

Mas como se calcula a taxa disseminação do vírus? De maneira resumida, a população é dividida em três grupos: suscetíveis, que podem contrair a doença; infecciosos, que carregam o vírus e podem transmiti-lo; removidos, que estão imunes ou morreram. A partir disso, usam-se inúmeras variáveis para calcular a curva de disseminação, como as características do vírus e seu modo de transmissão, além de condições sociais, demográficas e climáticas.

Um desafio na estatística é trabalhar com os parâmetros, e as variáveis corretas. Se conseguir determinar os parâmetros mais eficiente será minha simulação. Existem três principais variáveis para estimar o impacto de uma doença. Primeiro é preciso descobrir seu grau de contágio, calculando quantas pessoas podem ficar doentes a partir de uma pessoa já infectada, o chamado número básico de reprodução ou RO. Estudos apontam que o Covid-19 tem nível entre 2 a 4 – um primeiro infectado vai passar a doença para outros dois.

Outra variável é o Intervalo Serial, o tempo médio para que novos infectados manifestem sintomas. Quanto menor o intervalo, mais rapidamente a doença se alastra. Os sintomas do Covid-19, surgem em 4.4 dias em média. Por último a fatalidade da Covid-19 varia entre as faixas etárias e dispara nos grupos de risco, como idosos.

Quando trabalhamos com modelos estatísticos temos uma estimativa, não é 100% de certeza que isso ocorrerá, e a cada dia as variáveis mudam, Por exemplo Rio e São Paulo utiliza este modelo e o Governador do Rio de Janeiro já prorrogou três vezes a quarentena, e São Paulo irá prorrogar pela terceira vez também. Neste modelo matemático a cada dia, e cada semana temos uma nova variável diferente.

Conclusão

A matemática é sem dúvida uma ciência que está presente em tudo, por onde olhamos, andamos estamos cercados pelos números, e no combate ao covid-19 à contribuição da matemática está tendo uma grande importância, através de Modelos matemáticos estratégicos é essencial para se acompanhar não só a covid-19, mas também qualquer tipo de doença. Pois temos em mãos projeções que mostram com eficácia como podemos nos comportar e prevenir.

Fonte: Matemático Sousa